Tactical Tinkering

Fun with Prime Numbers (C++ console)

A good few years back I created a program to quickly generate prime numbers. I remember being pretty impressed with the speed I achieved. Alas, a hard drive failure caused this nice little bit of code to meet its end. I've now recreated it (and developed it further), and I'm fairly sure that the essence is pretty much the same as before, but it isn't as fast as I remember. Maybe I had some almighty inspiration all those years ago, leading to some incredibly clever and resourceful trick, or maybe it's just wishful thinking. Or maybe it was just a dream, and it never existed.

In any case, I present the new prime number generator, and successive improvements. It uses the sieve of Eratosthenes, and it's fairly fast, generating the first million primes in up to 90ms.

The basic algorithm — Version #1

You're probably well aware of the most basic primality test that exists: to test if a number $n$ is prime, divide it in turn by each of the numbers from 2 up to and including $\sqrt{n}$. If any of the results is a whole number then $n$ has a divisor and is not prime.

You'll also be well aware that this is an incredibly ineffficient method of generating prime numbers. A much better method is using a prime sieve, and here we use the simple and elegant sieve of Eratosthenes.

Here is the algorithm:

1. Start with a list of all integers from $2$ to $N$, the upper limit of your prime search.
2. Let $p=2$. Go through the list removing all multiples of, but not including, $p$.
3. Let $p=3$. Go through the list removing all multiples of, but not including, $p$.
4. Let $p=5$. Go through the list removing all multiples of, but not including, $p$.
5. Let $p=7$. Go through the list removing all multiples of, but not including, $p$.
6. Let $p=11$. Go through the list removing all multiples of, but not including, $p$.
7. ... you get the gist. Stop when $p>\sqrt{N}$. (For the same reason as in the basic primality test.)
8. Congratulations, the surviving numbers in your list are all the primes up to $N$!

• You'll notice that we let $p$ equal each sucessive prime number, starting with 2. In actual fact, we let $p$ be "the next number in the list", but it so happens that "the next number in the list" is the next prime number, as all numbers in between will already have been removed.
• In fact, after we've removed all multiples of $p$, all of the numbers in our list up to the square of the next prime will also be prime! For example, after we've sieved through with $p=7$, all numbers in our list up to (but not including) $11^2$ are prime. Hence, when we start sieving with $p=11$, the first multiple of $p$ we'll need to remove is $p^2=11^2=121$.

• We use a char array. Each char holds either a 1 (prime) or 0 (not prime), and the position of each char is the number it corresponds to. For example, the nth char in the array corresponds to the number n. So we use 1 byte of RAM for every number, so we can certainly get into the billions before we start running out of RAM, but that we do.


• On my (fairly old) laptop I can find:
  
  
  - 1 million primes (15,485,863) in 520ms.
  - 10 million primes (179,424,673) in 7.5s.
  - 50 million primes (982,451,653) in 44s.

Faster, faster! — Version #2

So, we're getting some not-too-shabby runtimes for our sieve. But we can do better that that!

The most glaringly obvious optimisation is with the list of candidates we start with: it's full of even numbers! Now, it's fairly obvious that no even number (except 2) can be prime, but lets analyse it in a slightly more complicated way (to a useful end, I promise!), with modular arithmetic. All natural numbers can be written in one of the following two ways: $$\left\{\begin{matrix} 2k\\ 2k+1 \end{matrix}\right.$$ However. Any number of the form $2k$ is obviously divisible by $2$, so the only form a prime number could take is $2k+1$.

So, by filling our initial array only with numbers of this form, we're not only halving the memory we need, but we're removing the need for the $p=2$ pass (which takes the longest).

So here's the code. VS2010 project file included. You can see that this version is more than twice as fast as version #1!

Why not do the same for $3$, and $5$, and $7$? Well, one quite convincing answer is that it starts getting very complicated very quickly! Let's including $3$. First we need a number divisble by $2$ and $3$. Since they're primes, the lowest common multiple of $2$ and $3$ is $2\times{}3=6$. Now, all natural numbers can be written in one of the following $6$ ways: $$\left\{\begin{matrix} 6k\\ 6k+1\\ 6k+2\\ 6k+3\\ 6k+4\\ 6k+5 \end{matrix}\right.$$ However, any number of the form $6k$ is divisible by both $2$ and $3$ (because we built it so). Then we can see that $6k+2$ and $6k+4$ are divisble by $2$, and $6k+3$ is divisible by $3$, so the only forms that a prime number could take are: $$\left\{\begin{matrix} 6k+1\\ 6k+5 \end{matrix}\right.$$ So now we only need to even consider $2/6$ of the natural numbers for primality!

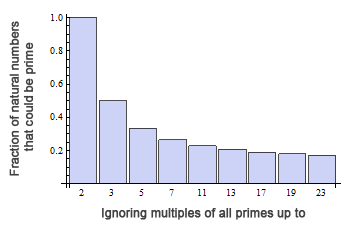
Like I said, you could include $5$ too, but then you'll have $lcm(2,3,5)=30$ different cases, $8$ of which could be prime. Include $7$ as well and you'll have $lcm(2,3,5,7)=210$ different cases, $48$ of which could be prime. It gets ugly very quickly, and the benefit of including each additional prime decays exponentially. Here's a graph.

It's all very well reducing the set of numbers we need to check for primality, but we haven't considered how our code must change to take this into account; and change it must.

Luckily, implementing the first improvement (ignoring all even numbers) was fairly easily. We let each successive char in our array correspond to each successive odd number. In cycling through the multiples of $p$ we simply skip every even multiple, i.e. increase by $2p$ each time. In this way, we can guarantee that we'll never see an even number, so we can directly map every number we come accross to the array — that is, the number $n$ will be represented by the $\frac{(n-1)}{2}$th char in the array — without having to waste precious operations first checking that $n$ is odd.

But we're not quite so lucky when we try to implement our next improvement — only accounting for numbers of the form $6k+1$ or $6k+5$.

Assume we fill our char array with pairs of numbers of the above form, i.e. $\left\{1,5,7,11,13,17,19,23,...\right\}$. Now, let's say we want to remove the $5th$ multiple of $13$, from our array. Which element in our array represents $117$? Well in this case the answer is none of them, since it's of the form $6k+3$. The point is, before we can remove any multiple from our array, we need to spend operations finding out if it's of the form $6k+1$, $6k+3$, or $6k+5$, and taking the modulus of every multiple would surely compromise any benefit.

Naturally I coded it anyway, in the name of tinkering, and it turns out that it's actually $\sim 25\%$ quicker! Here's the code, VS2010 project file included:

Taking the modulus of every multiple is obviously is less than ideal. The whole point of a sieve method is so we could do away with divisibility checks!

It occured to me that we should easily be able to keep track of each multiple's remainder mod 6 as we go along, since in cycling through the multiples we add a contant number each time. After some scribbling, I came up with the following:

Now for the moment of truth; did this make any difference? Here's the code, VS2010 project file included.

More, more! — Version #3

So, we've spent some time trying to make our prime generator as fast as possible, and I think we've done pretty well. We can find all the prime numbers up to 2,038,074,743 (yes, just over 2 billion!) in just over 30 seconds! That's fairly ridiculous if you think about it.

The problem is, there is a strict upper limit to the number of primes we can find in this way — determined purely by how much RAM we have available (ignoring virtual memory). On my old machine the 100 millionth prime is pretty much the limit. So what can we do about this?

Up till now we've been using a char array or 1's and 0's to keep track of whether a number is prime or not. In other words, we're using 4 bits of memory to hold a binary variable! This is silly, and requires fixing. Unfortunately, this necessitates more complicated, and therefore slower, code. But there we go.

Unhappily, there are no data types in C++ which take just one bit of memory (even a bool takes a whole byte) so we have to improvise: we use an int array, consider each int in its binary representation, and let each sucessive bit correspond to a number. For example, let the first int in he array represent the numbers from 1 to 32. Then, after removing all composite numbers, the int would end up as the following in its binary form (or the reverse, depending on which end you start from — here the leftmost bit represents 1, and the rightmost represents 32): $$ 0\,1\,1\,0\,1\,0\,1\,0\,0\,0\,1\,0\,1\,0\,0\,0\,1\,0\,1\,0\,0\,0\,1\,0\,0\,0\,0\,0\,1\,0\,1\,0 $$ Which, in its decimal form, is $6957218$.

So now we need a way to manipulate individual bits in any given int. Luckily, bitwise operations provide a fairly easy (and quite efficient) way to do this; see this tutorial for a good explanation of bitwise operators.

So, here's the code. VS2010 project file included. Just one note: I originally coded functions to perform the operations on the bit array, but as suggested in Steve Litt's excellent article, I thought I'd see if using macros instead made any significant difference. The result? Only a threefold speed increase!

Version #3.1, extending v2.1 (considering even numbers only) to use a bit array:

Even more?

A billion prime numbers is a lot. But as a percentage of how many primes exist it's ... well, zero. We can of course continue with this sieve method, but since we've run out of RAM our only option is to get the hard drive involved; sieving all numbers up to N, writing these results to a file, then moving on to the next N integers, and so on.

Alas, for the moment at least, this is where my own quest for the primes ends. But if you've got this far, you'll certainly want to take a look at Steve Litt's article, where he doesn't give up until he's found all primes up to 40 billion, and also discusses how one could get up to the really big numbers.

Useful Links

1. http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
2. The main ideas in this post came from this most excellent article by Steve Litt, which I strongly urge you to check out: http://www.troubleshooters.com/codecorn/primenumbers/primenumbers.htm
3. Tutorial on bitwise operators: http://www.cprogramming.com/tutorial/bitwise_operators.html

TOP PICKS

RECENT POSTS

INTERESTING LINKS